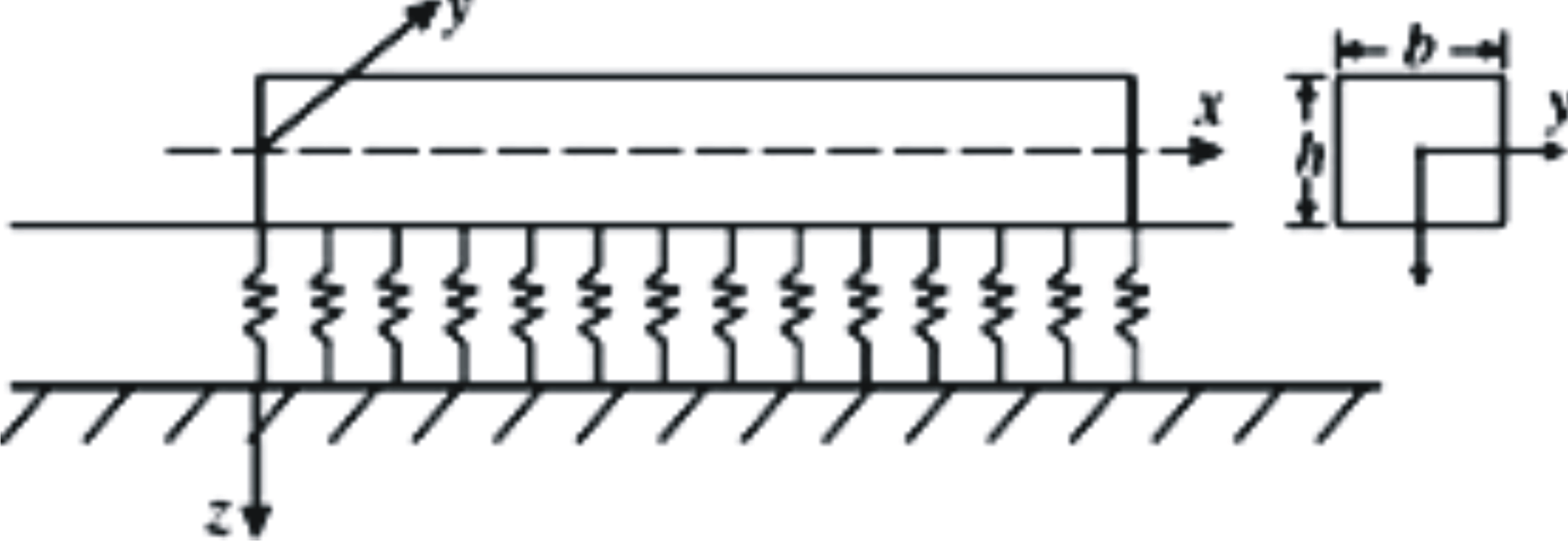
Stodola-Vianello method for the buckling load analysis of Euler-Bernoulli beam on Winkler foundation

Abstract

The critical buckling load determination for Euler-Bernoulli (EB) beams on elastic foundations is an important consideration in their analysis especially when they are subjected to in-plane compressive loads. This paper presents the Stodola-Vianello method for the iterative presentation and solution of the governing fourth order ordinary differential equation (ODE). The method of successive integrations is used after re-arrangement to express the governing ODE in iterative form. The eigenfunction for the nth buckling mode is used to obtain the (n + 1)th buckling mode equation for the Dirichlet end conditions considered. The condition for convergence at the nth buckling mode is used to drive the eigenequation, whose roots were used to find the buckling loads at the nth mode. The critical buckling mode is exact since the exact buckling mode function was used to derive it. The critical buckling load expression was expressed in standard form in terms of critical buckling load coefficients which depend on the parameter representing the EB beam on Winkler foundation interaction. The critical buckling load coefficients were found to be in close agreement with previously reported works, and identical with the exact critical buckling load coefficient obtained by previous researchers using closed form analytical methods.