A Hybrid Liu-Ridge Method of Handling Multicollinearity in Linear Regression Models

Abstract

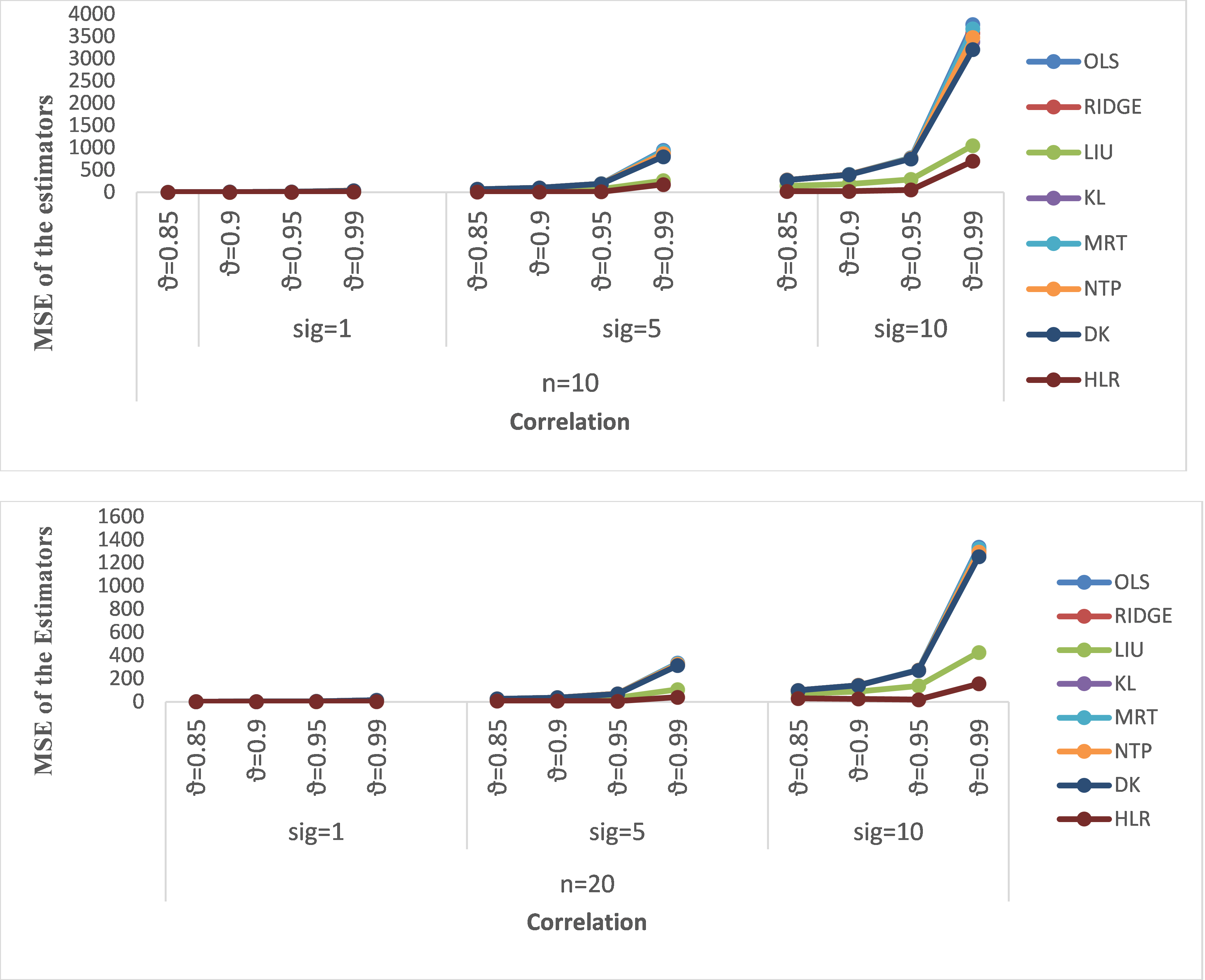
Multicollinearity is a critical challenge in linear regression analysis, causing instability and unreliability in Ordinary Least Squares (OLS) estimates when independent variables are highly correlated. While existing biased estimators, such as Ridge Regression, Liu Estimator, and Kibria-Lukman Estimator, partially address this issue, they often fall short of achieving optimal Mean Squared Error (MSE) performance across varying conditions. This study introduces the Hybrid Liu-Ridge (HLR) estimator, a novel integration of the Modified Ridge Type (MRT) and Modified Liu (MLIU) estimators, designed to robustly handle multicollinearity. A comprehensive theoretical analysis demonstrates the superiority of the HLR estimator, particularly in minimizing MSE compared to its predecessors. Performance evaluation via Monte Carlo simulations, conducted under varying multicollinearity levels, error variances, and sample sizes, confirms the consistency of the HLR estimator in outperforming existing methods. Real-world applications using agricultural and economic data further validate its robustness and practical utility. By offering improved reliability and adaptability, the HLR estimator represents a significant advancement in addressing multicollinearity, providing researchers and practitioners with a superior tool for regression analysis.